SNR Mode Contributions
What effect do the modes in a particular
SNR of two modes:
Consider two damped sinosoidal modes (a fundamental and an overtone) with an amplitude ratio $\alpha$ between the two modes. We set the two modes as
\[h(t) = h_0(t) + \alpha h_1(t)\]We can calculate the SNR under the assumptions that the noise is white, and hence for a quick and dirty approximation, use the normal $L^2$ inner product over the function space to be a measure of the squared SNR. We then have:
\[\begin{align} \rho^2 &= \langle h_0| h_0 \rangle + 2 \alpha \langle h_0| h_1 \rangle + \alpha^2 \langle h_1| h_1 \rangle \end{align}\]Assuming that
\[h(t | \omega, \gamma, \phi) = e^{-\gamma t} \cos(\omega t - \phi) \\\]or alternatively in terms of the quality factor:
\[h(t|Q\gamma, \gamma, \phi) = e^{-\gamma t}\cos(Q\gamma t - \phi)\] \[h(t) = h(t | Q_0\gamma_0, \gamma_0, \phi_0) + \alpha h(t | Q_1\gamma_1, \gamma_1, \phi_1)\]Plugging it in and using mathematica we get that the form of the squared SNR is, ofcourse quadratic in $\alpha$.
\[\rho^2 = C_0 + \alpha C_1 + \alpha^2 C_2\]Let
\[A = \frac{\gamma_0 Q_0 - \gamma_1 Q_1}{\gamma_0 + \gamma_1} \\ B = \frac{\gamma_0 Q_0 + \gamma_1 Q_1}{\gamma_0 + \gamma_1} \\\]Then:
\[C_0 = \frac{1}{4\gamma_0} \frac{1 + \cos(2\phi_0) + Q_0\sin(2\phi_0) + Q_0^2}{1 + Q_0^2}\] \[C_1 = \frac{1}{\gamma_0 + \gamma_1} \bigg(\frac{\cos(\phi_0 - \phi_1) + A \sin(\phi_0 - \phi_1)}{1 + A^2} + \frac{\cos(\phi_0 + \phi_1) + B \sin(\phi_0 + \phi_1)}{1 + B^2} \bigg)\] \[C_2 = \frac{1}{4\gamma_1}\bigg( \frac{1 + \cos \left(2 \phi _1\right) + Q_1 \sin \left(2 \phi _1\right) + Q_1^2}{1+ Q_1^2} \bigg)\]Checking the dependence of SNR on amplitude ratio
We checked the dependence of the SNR on the ampitude ratio for some specifically chosen signal parameters (but not any edge case ones), to see how it scales.
We set the first mode’s amplitude $A_0 = 10^{-20}$ and see the dependence of the SNR on $\alpha$. The noise that was injected was a particular realisation of the synthetic noise from GW150914. The rest of the parameters were fixed as below:
params = {
'model' : 'mchi',
'a' : np.array([A0, alpha*A0]),
'M': 100,
'chi': 0.7,
'modes': [(1,-2,2,2,0), (1,-2,2,2,1)],
'theta': [0.5, 0.3],
'ellip': [0.5,0.5],
'phi' : [0.2, 0.9],
'ra' : 1.95,
'dec': -1.27,
'psi': 0.82
}
Then we found the dependence of the SNR defined above and the amplitude ratio between the two modes given by $\alpha$.
We get the following plot for the SNR squared vs alpha:
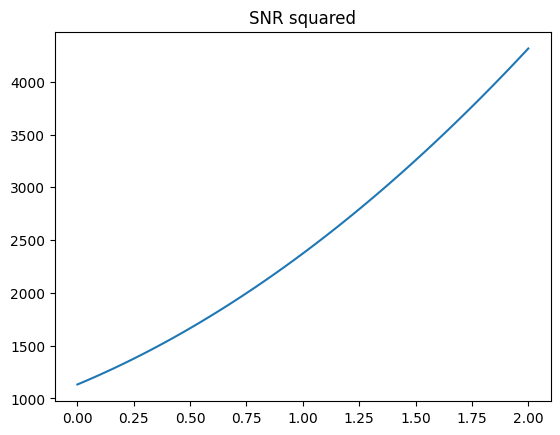
When we try to fit the above to the equation $\rho^2 \propto C_0 + C_1\alpha + C_2\alpha^2$, then we get the fit:
\[\rho^2 = 350.4 x^2 + 890.9 x + 1132\]Which gives the above graph.