Welcome to Computational Physics Final Project’s documentation!
Sampling spheres and spins
Notebooks, documentation for the sampler package can be found in the docs site for this repo
Final Project, Computational Physics, Fall 2023
Aditi Pujar, Asad Hussain, Kody Anderson, Shivan Mittal



Imagine a distribution \(\rho(\mathbf{x})\) over the domain \(\mathbf{x} \in X \subset \mathbb{R}^n.\) Sampling algorithms are answers to the question: Given that we do not have exact knowledge of the functional form of \(\rho,\) can we nonetheless generate samples from \(\rho?\) In particular, Markov Chain Monte Carlo algorithm is a sampling algorithm that only requires the knowledge of relative likelihood of two samples \(\mathbf{x}_1\) and \(\mathbf{x}_2\) drawn from the distribution \(\rho,\) i.e. knowledge of \({\rm Likelihood} = \rho(\mathbf{x}_1) / \rho(\mathbf{x}_2)).\) Hamiltonian Monte Carlo algorithm is another such sampling algorithm that further requires the knowledge of (a priori or empirically by differentiable ``code’’) the gradient of the likelihood. Numerous Physical problems can benefit from sampling algorithms. These range from (Classical and Quantum) many-body problems to data analysis for large scale Physics experiments (LIGO, CERN).
to package our own Markov Chain Monte Carlo algorithm and existing Hamiltonian Monte Carlo algorithm from
blackjaxlibrary into a single class interface, andto demonstrate the ease of use of out interface and the utility of the sampling algorithms via the following examples of,
Plots from our work

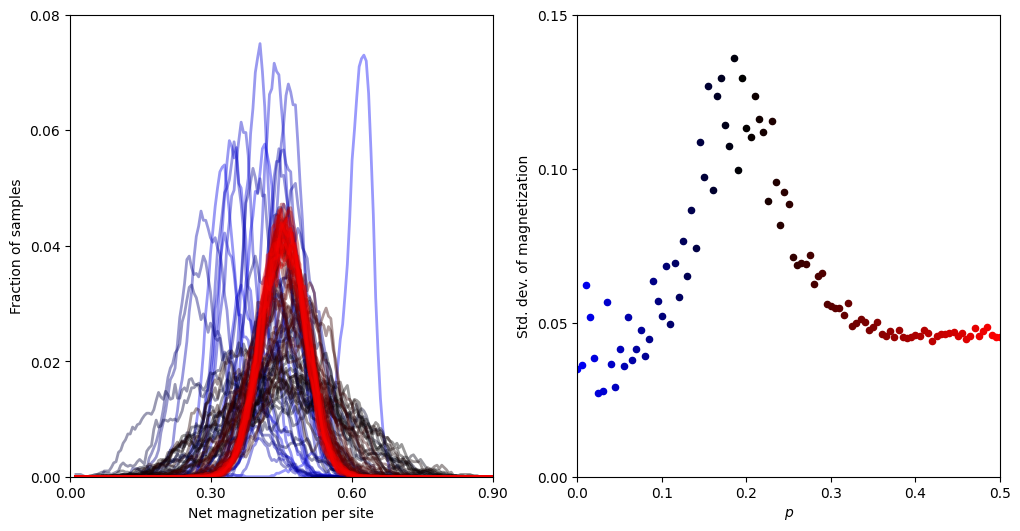
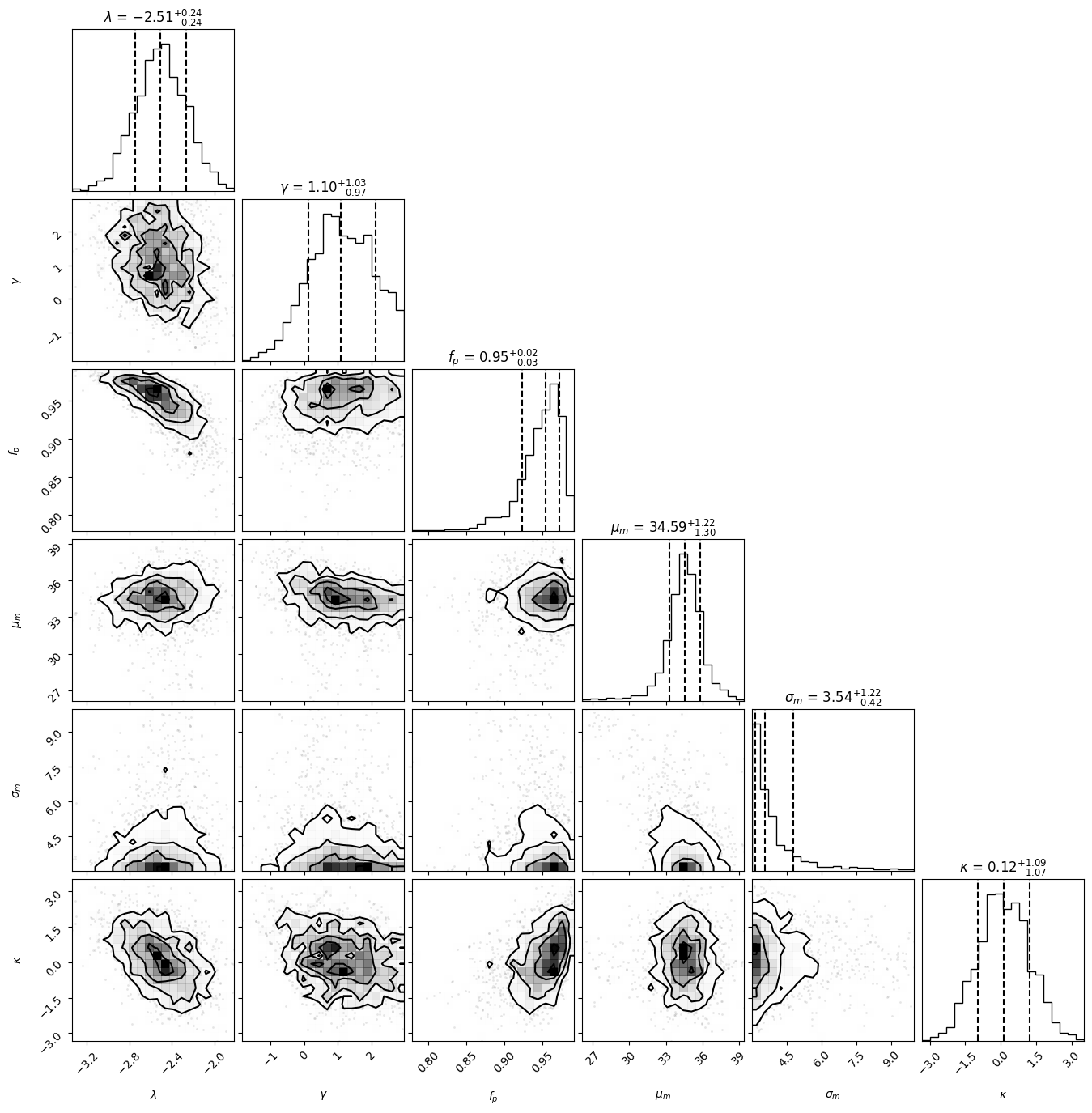
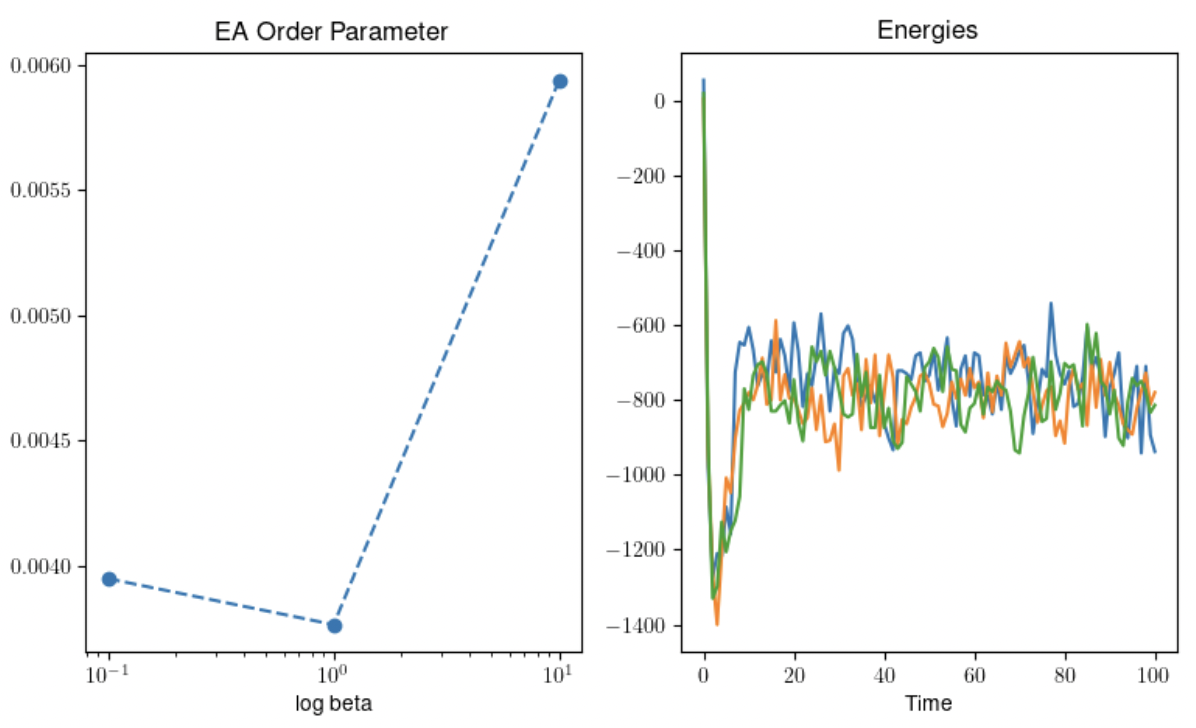
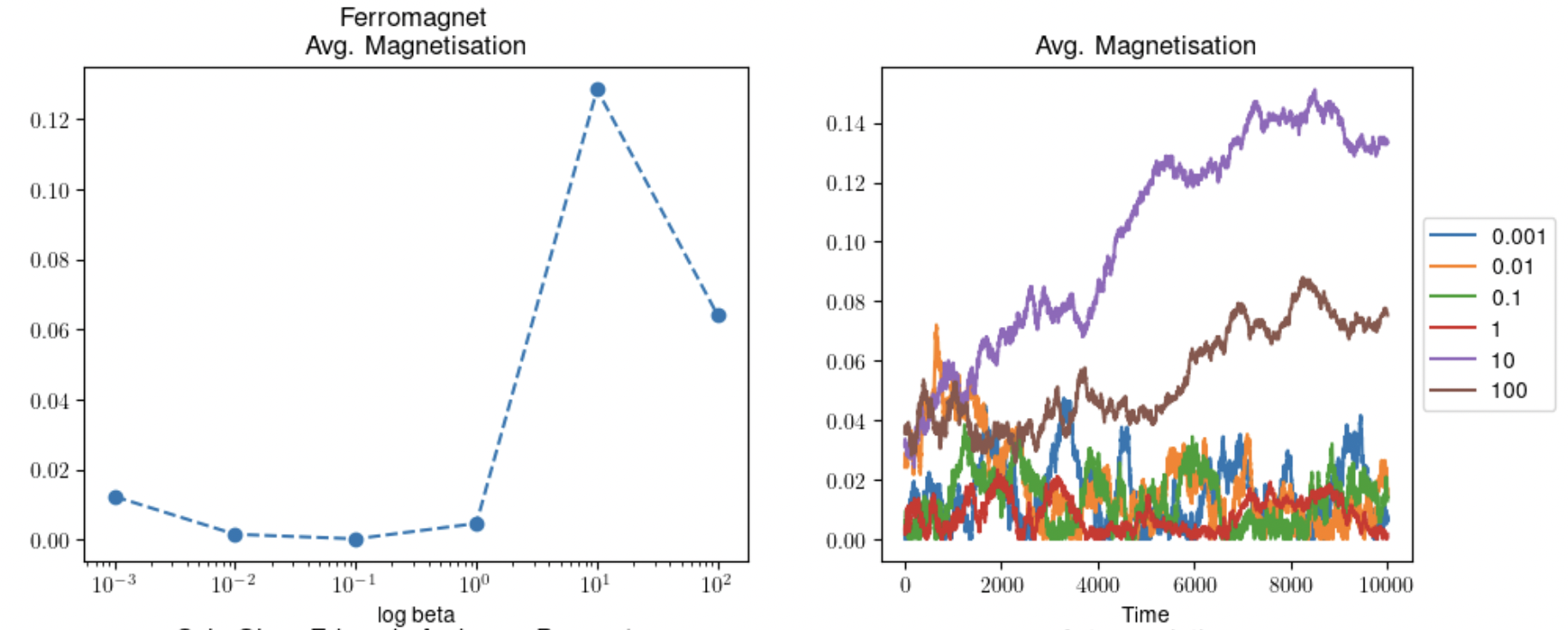
Contents:
- Soft-sphere packing
- Continuous MH Sampler
- Simple Bayesian Inference Examples
- Inferring the Distribution of Gravitational Waves
- 1D Quantum spin chains
- quicksampler